改良したアプリをこちらに掲載
https://riragon.com/sosu-seisei-sieve/
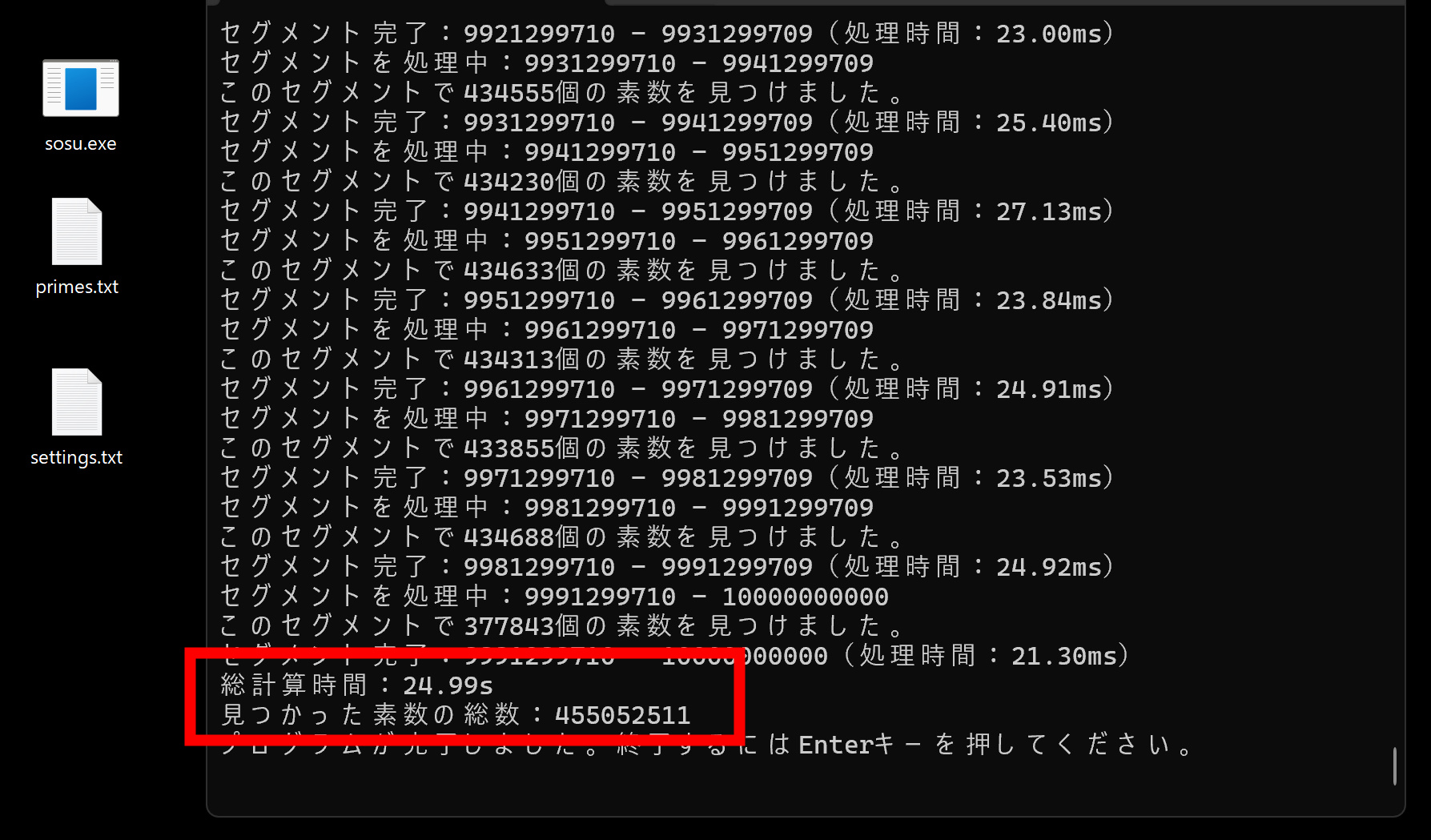
20秒で1から100億(10,000,000,000)の11桁の自然数の中から、素数4億5505万2,511(455,052,511)個を見つけるRustプログラムを作ってみました。ネットワークやGPUを使ったりアルゴリズムを改良することでもっと高速になるでしょう。
本記事の趣旨は、ChatGPTなどのAIの可能性についてです。AIにはプログラムの有無を問わず専門分野の研究を加速させる力があるでしょう。学生や子供でも世界的な発見ができる新しい時代を感じます。まさに新しいツールです。
私は素数やRustに関しては初心者です。プログラムもPythonのひどく疎かな基礎知識しかありません。素数が1とその数自身でしか割り切れない数であることを昨日初めて学びました。そして今日プログラムを作ったのです。
またWebでは素数のサンプルは5000万個ぐらいまでしかDLできません。自分でコードを作成すれば好きなだけ素数のサンプルを出力できます。
巨大な素数生成実行ファイル
巨大な素数生成アプリが公開されていない気がするので、今回作成した素数生成実行ファイル(windows用sosu.exe)をついでにアップしておきます。80億個ぐらいの素数を10分ぐらいで出力できました。もっと大きなファイルも作れるでしょう。あらゆる点において野良アプリなので自己責任でつかってください。
巨大な素数生成アプリsosu.exe
https://drive.google.com/file/d/11AgM0K1s4dKwndOs4Q2OJ93BKbAo7vJE/view?usp=drive_link
素数のおもしろい特徴
素数は数字の末尾がかならず1、3、7、9になります。その1、3、7,9だけに注目すると出現比率は大体25%になり、素数はランダムに見えます。しかし2016年にサウンダララジャン氏が末尾の数字が連続した場合、次に同じ数字がくる確率が低いことを論文として発表しました。
https://arxiv.org/abs/1603.03720
以下記事など分かりやすく紹介されています。※もし完全にランダムであれば、同じ数字が連続した場合でも次にくる数字の出現頻度は同じになるのです。
https://www.itmedia.co.jp/news/articles/2407/04/news044.html
https://www.gizmodo.jp/2016/03/prime-number-not-so-random.html
2016年以前からも素数には何らかの潜在的な規則性やパターンが存在するとされており、リーマン予想や素数定理、ハーディ・リトルウッド予想などが知られています。まあ、意味が良く分からないですよね。こんなことプログラムも数学もできない庶民には、1mmも理解できません。
今の時代はChatGPT O1-PreviewやO1-miniがあるじゃないですか。実際に素数がランダムではないということを検証してみましょう。つまりChatGPT O1-PreviewやO1-miniがあれば、小学生でも2016年に発見したことを発見できてしまう可能性があるということです。
Rustで素数を発見するプログラムを作る
素数を効率よく見つけるために、もっとも一般的なエラトステネスのふるいを使用しています。素数は末尾が1、3、7、9になり、4で割った余りが1または3です。もっと簡単に言えば素数が2の倍数(偶数)でも5の倍数でもないということです。プログラムでは、2と5の倍数を計算対象から初めから除外しています。
さらにプログラムはエラトステネスのふるいを改良して、指定した個数まで小さな素数を事前に計算しメモリ内のベクターに保存します。これらの倍数を大きな数範囲の素数探索に利用しています。
複数のCPUを同時に使えるように並列処理、エラトステネスのふるいのセグメント化、バッファリング、設定項目の外部ファイル化などを実装しました。以下Rustのコードです。
使い方を簡単に紹介します。Rustの環境をUbuntuで構築します。
curl --proto '=https' --tlsv1.2 -sSf https://sh.rustup.rs | sh
source $HOME/.cargo/env
sudo rustup target add x86_64-pc-windows-gnu
sudo apt install mingw-w64
cargo new sosu
cd sosuCargo.tomlとsrc/main.rsをコピーして、実行すれば計算が開始されます。Windows用の実行ファイルとしてexeファイルも書き出せますが今回は説明しません。
cargo run --releasecargo run –releaseで実行するとsettings.txtが作成されます。これが初期設定です。設定を変えたい場合は書き換えてください。primes.txtには発見した素数が記載されています。巨大なので普通のエディタでは開けません。※primes.txtを普通のエディタで開きたいときはprime_maxを1000とか10000ぐらいに小さくしてください。prime_cache_sizeも100とか1000とか。文字化けするかも。なにかエディタツールで開くのがよいでしょう。
settings.txtの項目説明
prime_cache_size = 100000
segment_size = 10000000
chunk_size = 16384
writer_buffer_size = 8388608
prime_max = 10000000000prime_cache_size = 100000
最初に生成する素数の数を指定します。この値までの素数を計算しメモリ内にキャッシュします。これらの素数は後続の計算で、より大きな数の範囲における素数判定の基準として使用されます。小さい素数のエラトステネスのふるいを用いて大きな数の範囲内で素数の倍数を除外することで、計算量が大幅に削減され、全体の効率が向上します。
segment_size = 10000000
セグメント化されたエラトステネスのふるいで一度に処理する数の範囲を定義します。セグメント化することにより、メモリ使用量を管理しやすくなり、大きな数範囲を効率良く処理できるようになります。各セグメントは独立して処理できるため、並列処理や分散処理にも適しています。
chunk_size = 16384
並列処理する際に分割する各チャンクのサイズを指定します。プログラムは、セグメント内の数をさらにこのサイズのチャンクに分割し、それぞれのチャンクを個別に並列処理します。チャンクサイズを適切に設定することで、多核プロセッサの能力を最大限に活用でき、ロードバランシングを改善し、処理速度を向上させることができます。
writer_buffer_size = 8388608
ファイルへの書き込みを行う際に使用するバッファのサイズ(バイト単位)を指定します。ここでは8MBのバッファが割り当てられます。ファイルI/Oの効率を向上させるために、大きなバッファを使用してディスクへの書き込みをバッチ処理します。これにより、I/Oの待ち時間が減少し、全体のパフォーマンスが向上します。
prime_max = 10000000000
プログラムが探索する最大の数を定義します。素数探索の範囲を事前に定義することで、プログラムの実行計画を適切に立て、必要なリソースを見積もり、期待される結果を計画的に得ることができます。10000000000は100億です。
利用する環境に合わせて数値を調整できます。
Rustで素数を発見してみよう
素数のテキストは思ったより容量が大きいのです。Webで素数のダウンロードを検索しても最大で5,000万個ぐらいの素数しか見つかりません。少ない?自分でプログラムを走らせれば、20秒ぐらいで4億個ぐらい発見できます。
100億の数字の中から、25秒で455052511個の素数を発見しました。cpuはGen Intel(R) Core(TM) i9-13980HXです。ちなみにテキストのファイルサイズは4.6GBもあります。無駄に大きい!
サウンダララジャン氏が末尾の数字が連続した場合、次に同じ数字がくる確率が低いことを検証してみた
455052511個の素数が入手できたので、末尾の数字が連続した場合、次に同じ数字がくる確率が低いことを再検証してみました。455052511個の素数を分析します。
※普通に1、3,7,9の出現率を求めたところ数を増やすと、ほぼ25%の出現比率でした。
10桁の素数(404204977個)に対する各桁位置の数字出現頻度(%)とカウント:
末尾の数字の出現頻度(%)とカウント:
数字 0: 0.00% (0)
数字 1: 25.00% (101050133)
数字 2: 0.00% (0)
数字 3: 25.00% (101053126)
数字 4: 0.00% (0)
数字 5: 0.00% (0)
数字 6: 0.00% (0)
数字 7: 25.00% (101051725)
数字 8: 0.00% (0)
数字 9: 25.00% (101049993)
以下455052511個中、連続した末尾の場合何が来るか出現頻度を求めたものです。1、3,7,9,それぞれで10回連続まで求めました。プログラムは掲載しません。気になる人はコードを作ってお試しください。
末尾が1
末尾が1の素数が1回連続で終わった後の次の素数の末尾の総数: 113761519
次の素数の末尾の出現頻度:
末尾が1: 18.83% (21423878)
末尾が3: 29.43% (33479893)
末尾が7: 29.62% (33692895)
末尾が9: 22.12% (25164853)
末尾が1の素数が2回連続で終わった後の次の素数の末尾の総数: 21423878
次の素数の末尾の出現頻度:
末尾が1: 16.88% (3615401)
末尾が3: 31.29% (6704060)
末尾が7: 28.78% (6166159)
末尾が9: 23.05% (4938258)
末尾が1の素数が3回連続で終わった後の次の素数の末尾の総数: 3615401
次の素数の末尾の出現頻度:
末尾が1: 16.40% (592917)
末尾が3: 31.53% (1139757)
末尾が7: 29.50% (1066418)
末尾が9: 22.58% (816309)
末尾が1の素数が4回連続で終わった後の次の素数の末尾の総数: 592917
次の素数の末尾の出現頻度:
末尾が1: 15.64% (92705)
末尾が3: 31.78% (188433)
末尾が7: 29.57% (175306)
末尾が9: 23.02% (136473)
末尾が1の素数が5回連続で終わった後の次の素数の末尾の総数: 92705
次の素数の末尾の出現頻度:
末尾が1: 15.21% (14097)
末尾が3: 31.66% (29347)
末尾が7: 29.77% (27602)
末尾が9: 23.36% (21659)
末尾が1の素数が6回連続で終わった後の次の素数の末尾の総数: 14097
次の素数の末尾の出現頻度:
末尾が1: 15.06% (2123)
末尾が3: 31.40% (4426)
末尾が7: 30.03% (4233)
末尾が9: 23.52% (3315)
末尾が1の素数が7回連続で終わった後の次の素数の末尾の総数: 2123
次の素数の末尾の出現頻度:
末尾が1: 16.63% (353)
末尾が3: 30.90% (656)
末尾が7: 29.82% (633)
末尾が9: 22.66% (481)
末尾が1の素数が8回連続で終わった後の次の素数の末尾の総数: 353
次の素数の末尾の出現頻度:
末尾が1: 16.71% (59)
末尾が3: 28.33% (100)
末尾が7: 30.03% (106)
末尾が9: 24.93% (88)
末尾が1の素数が9回連続で終わった後の次の素数の末尾の総数: 59
次の素数の末尾の出現頻度:
末尾が1: 8.47% (5)
末尾が3: 30.51% (18)
末尾が7: 45.76% (27)
末尾が9: 15.25% (9)
末尾が1の素数が10回連続で終わった後の次の素数の末尾の総数: 5
次の素数の末尾の出現頻度:
末尾が1: 0.00% (0)
末尾が3: 20.00% (1)
末尾が7: 60.00% (3)
末尾が9: 20.00% (1)
末尾が3
末尾が3の素数が1回連続で終わった後の次の素数の末尾の総数: 113765625
次の素数の末尾の出現頻度:
末尾が1: 24.19% (27517671)
末尾が3: 18.23% (20741925)
末尾が7: 27.97% (31818060)
末尾が9: 29.61% (33687968)
末尾が3の素数が2回連続で終わった後の次の素数の末尾の総数: 20741925
次の素数の末尾の出現頻度:
末尾が1: 25.24% (5234812)
末尾が3: 17.13% (3553485)
末尾が7: 28.06% (5819248)
末尾が9: 29.57% (6134380)
末尾が3の素数が3回連続で終わった後の次の素数の末尾の総数: 3553485
次の素数の末尾の出現頻度:
末尾が1: 25.40% (902745)
末尾が3: 16.45% (584632)
末尾が7: 28.40% (1009296)
末尾が9: 29.74% (1056812)
末尾が3の素数が4回連続で終わった後の次の素数の末尾の総数: 584632
次の素数の末尾の出現頻度:
末尾が1: 25.89% (151361)
末尾が3: 15.71% (91818)
末尾が7: 28.59% (167125)
末尾が9: 29.82% (174328)
末尾が3の素数が5回連続で終わった後の次の素数の末尾の総数: 91818
次の素数の末尾の出現頻度:
末尾が1: 26.07% (23937)
末尾が3: 15.07% (13838)
末尾が7: 28.71% (26363)
末尾が9: 30.15% (27680)
末尾が3の素数が6回連続で終わった後の次の素数の末尾の総数: 13838
次の素数の末尾の出現頻度:
末尾が1: 25.69% (3555)
末尾が3: 15.17% (2099)
末尾が7: 28.72% (3974)
末尾が9: 30.42% (4210)
末尾が3の素数が7回連続で終わった後の次の素数の末尾の総数: 2099
次の素数の末尾の出現頻度:
末尾が1: 25.77% (541)
末尾が3: 14.58% (306)
末尾が7: 28.54% (599)
末尾が9: 31.11% (653)
末尾が3の素数が8回連続で終わった後の次の素数の末尾の総数: 306
次の素数の末尾の出現頻度:
末尾が1: 27.45% (84)
末尾が3: 14.71% (45)
末尾が7: 23.86% (73)
末尾が9: 33.99% (104)
末尾が3の素数が9回連続で終わった後の次の素数の末尾の総数: 45
次の素数の末尾の出現頻度:
末尾が1: 24.44% (11)
末尾が3: 20.00% (9)
末尾が7: 28.89% (13)
末尾が9: 26.67% (12)
末尾が3の素数が10回連続で終わった後の次の素数の末尾の総数: 9
次の素数の末尾の出現頻度:
末尾が1: 33.33% (3)
末尾が3: 11.11% (1)
末尾が7: 33.33% (3)
末尾が9: 22.22% (2)
末尾が7
末尾が7の素数が1回連続で終わった後の次の素数の末尾の総数: 113764039
次の素数の末尾の出現頻度:
末尾が1: 25.46% (28959412)
末尾が3: 26.89% (30589282)
末尾が7: 18.22% (20731084)
末尾が9: 29.43% (33484260)
末尾が7の素数が2回連続で終わった後の次の素数の末尾の総数: 20731084
次の素数の末尾の出現頻度:
末尾が1: 24.67% (5114113)
末尾が3: 26.74% (5543259)
末尾が7: 17.13% (3551409)
末尾が9: 31.46% (6522303)
末尾が7の素数が3回連続で終わった後の次の素数の末尾の総数: 3551409
次の素数の末尾の出現頻度:
末尾が1: 24.54% (871366)
末尾が3: 27.04% (960152)
末尾が7: 16.46% (584595)
末尾が9: 31.97% (1135296)
末尾が7の素数が4回連続で終わった後の次の素数の末尾の総数: 584595
次の素数の末尾の出現頻度:
末尾が1: 24.56% (143572)
末尾が3: 27.06% (158217)
末尾が7: 15.79% (92316)
末尾が9: 32.58% (190490)
末尾が7の素数が5回連続で終わった後の次の素数の末尾の総数: 92316
次の素数の末尾の出現頻度:
末尾が1: 25.03% (23104)
末尾が3: 27.07% (24991)
末尾が7: 15.22% (14047)
末尾が9: 32.69% (30174)
末尾が7の素数が6回連続で終わった後の次の素数の末尾の総数: 14047
次の素数の末尾の出現頻度:
末尾が1: 25.55% (3589)
末尾が3: 26.80% (3764)
末尾が7: 15.13% (2125)
末尾が9: 32.53% (4569)
末尾が7の素数が7回連続で終わった後の次の素数の末尾の総数: 2125
次の素数の末尾の出現頻度:
末尾が1: 26.40% (561)
末尾が3: 27.81% (591)
末尾が7: 15.01% (319)
末尾が9: 30.78% (654)
末尾が7の素数が8回連続で終わった後の次の素数の末尾の総数: 319
次の素数の末尾の出現頻度:
末尾が1: 27.90% (89)
末尾が3: 29.78% (95)
末尾が7: 13.17% (42)
末尾が9: 29.15% (93)
末尾が7の素数が9回連続で終わった後の次の素数の末尾の総数: 42
次の素数の末尾の出現頻度:
末尾が1: 35.71% (15)
末尾が3: 19.05% (8)
末尾が7: 16.67% (7)
末尾が9: 28.57% (12)
末尾が7の素数が10回連続で終わった後の次の素数の末尾の総数: 7
次の素数の末尾の出現頻度:
末尾が1: 28.57% (2)
末尾が3: 28.57% (2)
末尾が7: 28.57% (2)
末尾が9: 14.29% (1)
末尾が9
末尾が9の素数が1回連続で終わった後の次の素数の末尾の総数: 113761326
次の素数の末尾の出現頻度:
末尾が1: 31.52% (35860558)
末尾が3: 25.45% (28954524)
末尾が7: 24.19% (27521999)
末尾が9: 18.83% (21424245)
末尾が9の素数が2回連続で終わった後の次の素数の末尾の総数: 21424245
次の素数の末尾の出現頻度:
末尾が1: 33.71% (7222175)
末尾が3: 24.47% (5241940)
末尾が7: 24.95% (5345419)
末尾が9: 16.87% (3614711)
末尾が9の素数が3回連続で終わった後の次の素数の末尾の総数: 3614711
次の素数の末尾の出現頻度:
末尾が1: 34.43% (1244546)
末尾が3: 24.55% (887541)
末尾が7: 24.60% (889325)
末尾が9: 16.41% (593299)
末尾が9の素数が4回連続で終わった後の次の素数の末尾の総数: 593299
次の素数の末尾の出現頻度:
末尾が1: 34.93% (207221)
末尾が3: 24.45% (145062)
末尾が7: 24.97% (148169)
末尾が9: 15.65% (92847)
末尾が9の素数が5回連続で終わった後の次の素数の末尾の総数: 92847
次の素数の末尾の出現頻度:
末尾が1: 35.16% (32648)
末尾が3: 24.62% (22858)
末尾が7: 25.14% (23340)
末尾が9: 15.08% (14001)
末尾が9の素数が6回連続で終わった後の次の素数の末尾の総数: 14001
次の素数の末尾の出現頻度:
末尾が1: 35.06% (4909)
末尾が3: 25.16% (3523)
末尾が7: 25.11% (3516)
末尾が9: 14.66% (2053)
末尾が9の素数が7回連続で終わった後の次の素数の末尾の総数: 2053
次の素数の末尾の出現頻度:
末尾が1: 34.53% (709)
末尾が3: 25.38% (521)
末尾が7: 26.21% (538)
末尾が9: 13.88% (285)
末尾が9の素数が8回連続で終わった後の次の素数の末尾の総数: 285
次の素数の末尾の出現頻度:
末尾が1: 33.68% (96)
末尾が3: 24.56% (70)
末尾が7: 31.58% (90)
末尾が9: 10.18% (29)
末尾が9の素数が9回連続で終わった後の次の素数の末尾の総数: 29
次の素数の末尾の出現頻度:
末尾が1: 41.38% (12)
末尾が3: 27.59% (8)
末尾が7: 27.59% (8)
末尾が9: 3.45% (1)
末尾が9の素数が10回連続で終わった後の次の素数の末尾の総数: 1
次の素数の末尾の出現頻度:
末尾が1: 0.00% (0)
末尾が3: 100.00% (1)
末尾が7: 0.00% (0)
末尾が9: 0.00% (0)
以上からとても面白い特徴が分かります。もしランダムなら数字が連続する場合に他の数字より出現頻度が下がることはありません。明らかに何か法則があるので出現が下がるといえます。
1、3、7,9の出現はほとんどランダムに近いです。しかし連続する場合は、連続する数字が出にくくなり、他の数字が出やすく循環するような出現になっています。そのため連続する場合は数字に偏りがあるが、1、3、7,9の出現はほとんどランダムに近いということが分かります。おもしろいですね。
また同じ数字が続く場合、さらに出現しにくくなります。素数の数がある程度大きくなるとその傾向はなくなりそうです。
まったくの数学初心者&プログラム初心者がわずか2日でここまで分析できました。もし1カ月ぐらい毎日何か法則を探したら、いまだ発見されていない傾向を見つけられるかもしれません。
小学生でも2016年の発見のように、わかりやすい面白い今までの概念を覆す何かを見つけられるかもしれません。もちろん数学や学術的な基礎がなければ、それを見つけても何も証明できないでしょう。すごい時代が来ましたね。
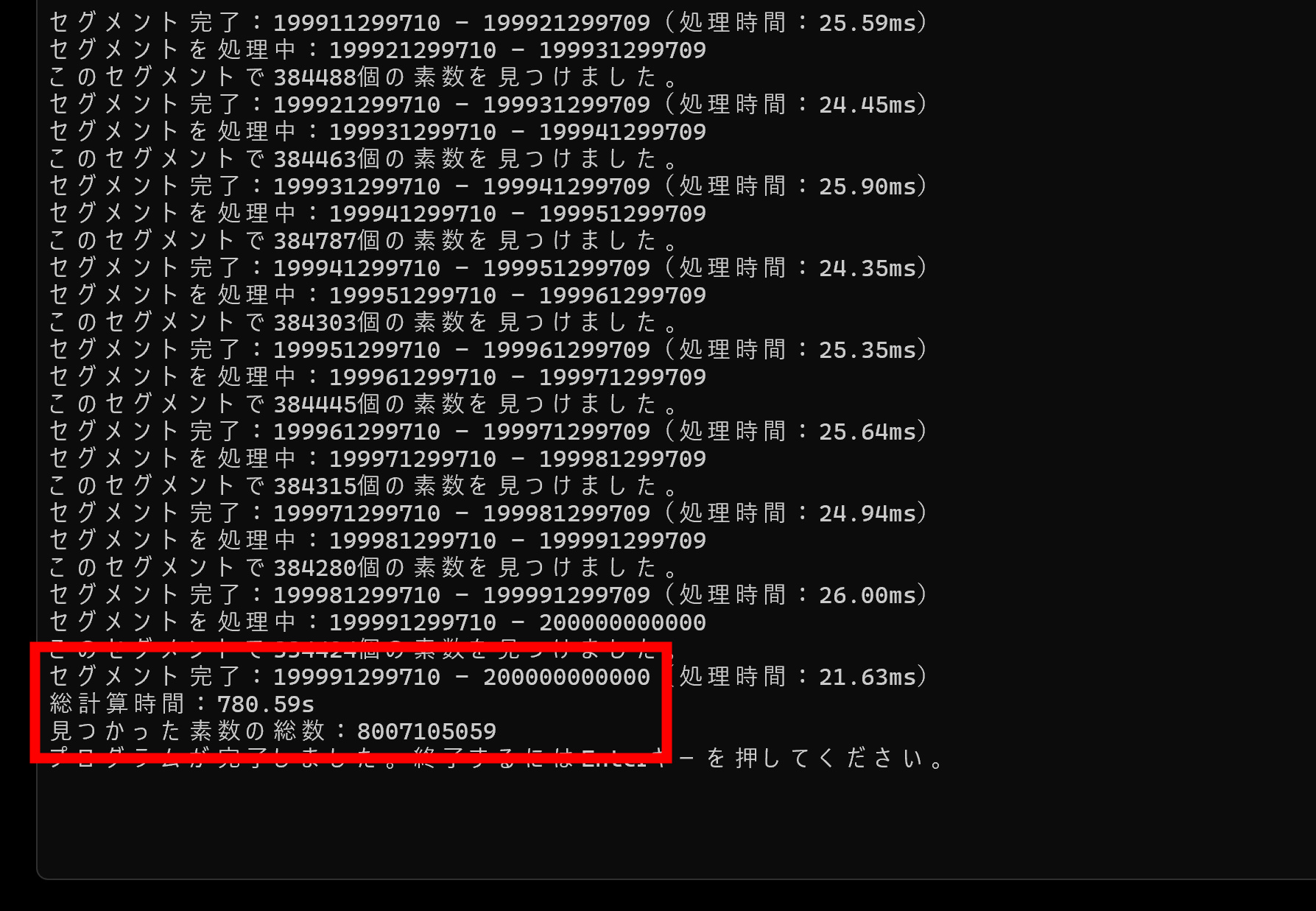
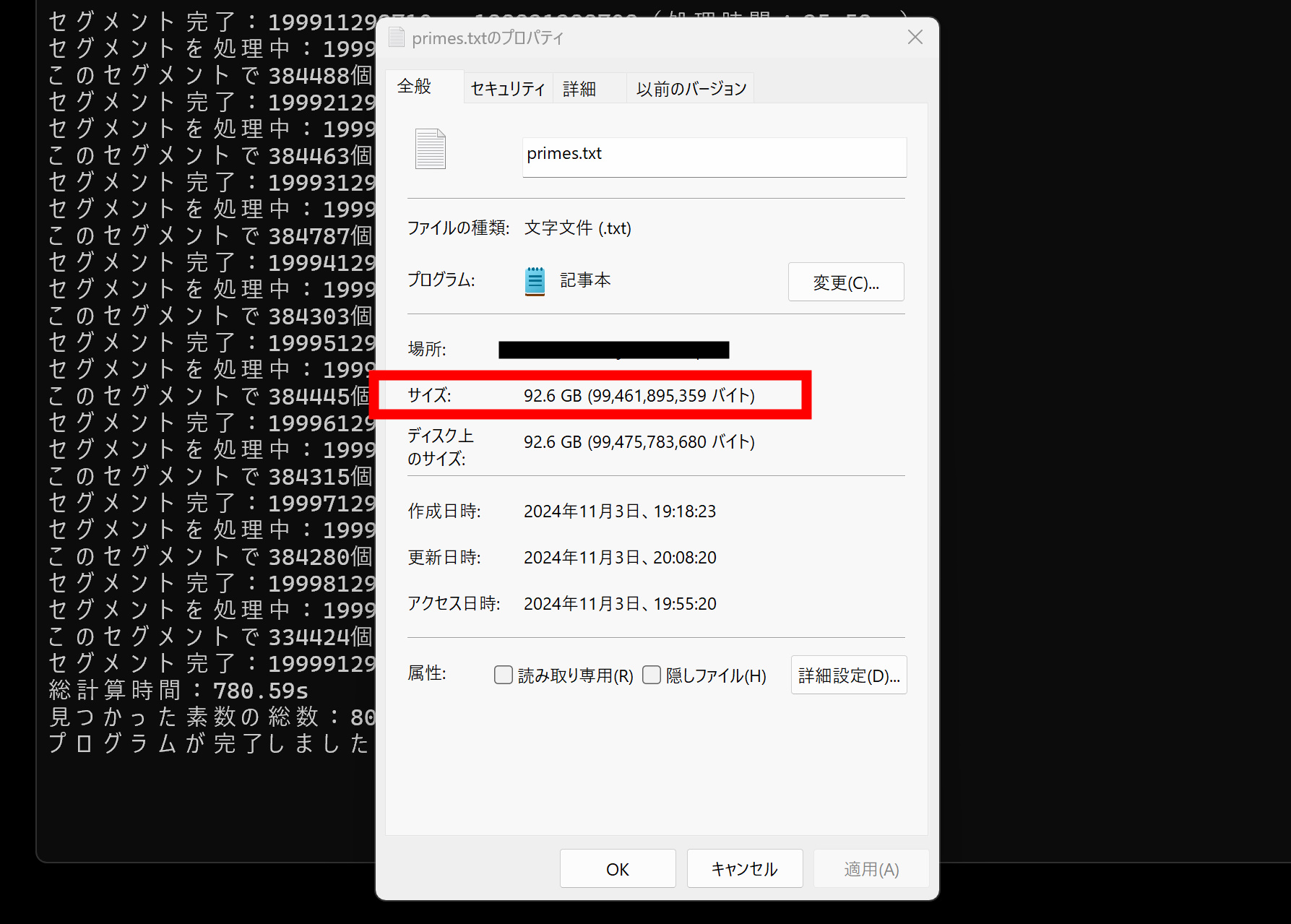
最後に検証で780秒、200,000,000,000(2千億)で、8,007,105,059個の素数でした。ファイルサイズは92GBです。すべての数字が正しいかは未検証ですが、たぶん正しいのでは?小さい数字では確認しました。