月額200$にてcursorアプリ制作チャレンジをしています。課金1ヵ月目のプロダクトは「sosu-seisei-2」です。フルRust製のアプリケーションです。
巨大範囲の素数リストを高速に作れるGenerator機能と、素数の性質を体験できる分析ツール群 π(x) / Gap / Density / Spiral機能を備えています。手軽に高校~大学レベルの素数の分布を確認できます。起動もWidnowsでexeを実行するだけです。専用ツールをUbuntuなどでビルドしなくてすぐにWindowsで体験できます。
githubのリリースページからexeをDLできます。ソースコードも公開しています。
https://github.com/riragon/sosu-seisei-2
https://github.com/riragon/sosu-seisei-2/releases/tag/exe
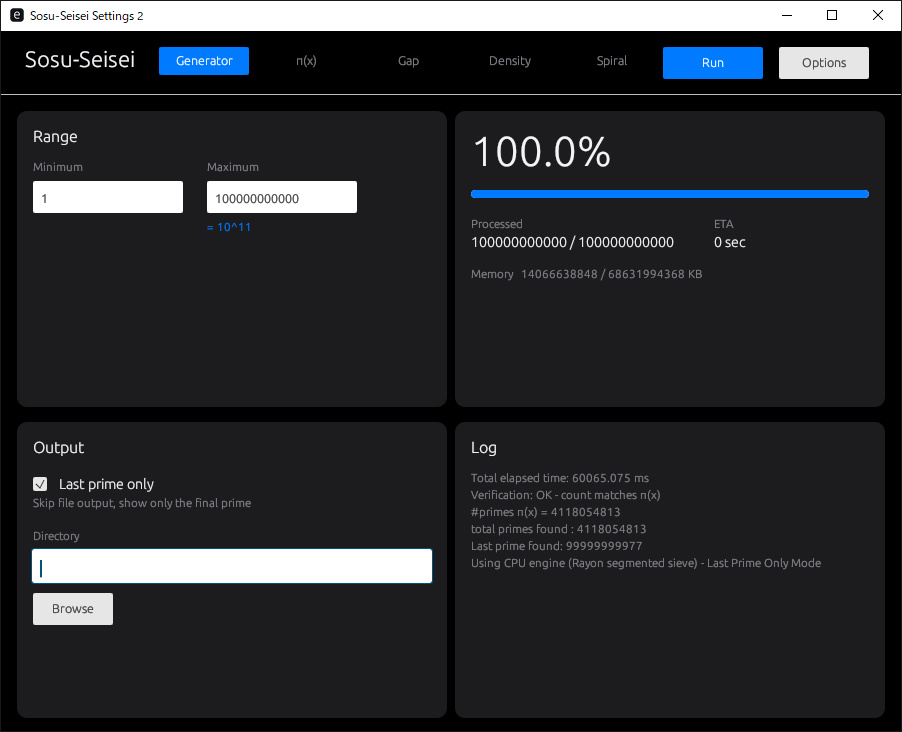
巨大な素数リストを作れるGenerator機能は、だいぶ高速化してあります。10の11乗 (1000億)に含まれる素数は約41億個あります。1分ぐらいで生成できます。さらに100倍ぐらいのサイズも作れるはずです。簡単にこの量のデータをローカルで扱えること自体が珍しいでしょう。この素数リストを自分の Python / Rust / C++ / GPU処理などに読み込めば、独自の切り口で分析できます。
使い方は簡単です。数字の範囲を指定してRunするだけです。オプションなど細かい機能もあります。指定したフォルダーに書き出せます。Last prime onlyは書き出さないモードなので、書き出したいときは☑を外しましょう。
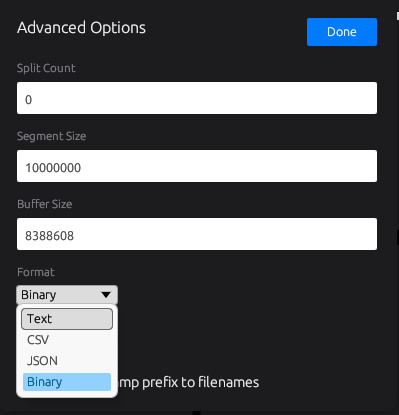
素数のフォーマットはText、CSV、JSON、Binaryなどを選べます。Binaryにすると無駄がなくて速いです。
たくさんの素数が一瞬で自分のデスクトップに作られます。次に体験できる分析ツールを紹介します。
π(x)タグで素数の法則性を体験
π(x)タブでは、1からxまでに素数が何個あるか(π(x))を数えてグラフにします。あわせて、だいたいこれくらいになりそうという予想(x/log x)とも比較できます。比較の見せ方は2通りあり、π(x)とx/log xを重ねて表示するモードと、π(x)をx/log xで割った比率を表示するRatioモードがあります。Ratioモードでは、1にどれだけ近いかが1本の線で分かります。
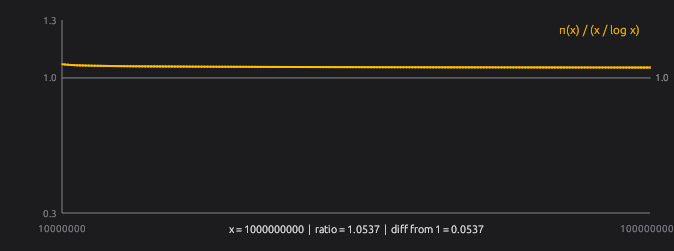
素数はバラバラに出てきて、次に出る素数は当てられません。でも、たくさん集めて数えると大きなルールが見えてきます。体感できる不思議さはここです。xを大きくすると、予想に対する比率は全体として1に近づく傾向が見えてきます。ただし近づき方は一直線ではなく、上下にゆらゆら揺れます。
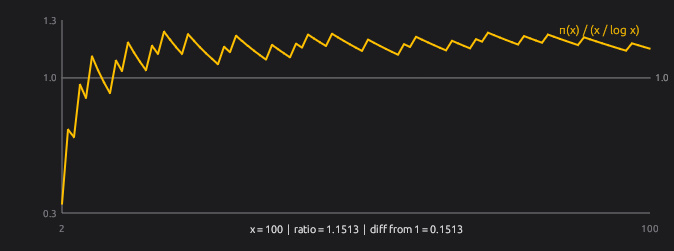
素数1個ずつは気まぐれみたいなのに、全体ではちゃんと決まりがあります。実は単純なx/log xという予想と驚くほど似ているんです。素数は、近くを見ると読めないのに、遠くから見ると法則に従う。そんな矛盾したような性格がπ(x)で見えてきます。予測できない素数が x/log x とそっくりな不思議です。何か素数には法則がある気がしませんか?
Gapタブで素数の間隔の不思議を体験
Gapタブでは、連続する素数同士の差、つまり素数ギャップを集めて、どのギャップがどれくらい出るのかをヒストグラムで表示します。表示はLinearとLogを切り替えられます。Linearでは小さいギャップの多さが直感的に分かり、Logでは回数の少ない大きなギャップまで形として見えます。
素数は次が分からないので、ギャップもバラバラに見えます。ところが、たくさん集めてみると、よく出るギャップと出にくいギャップがはっきり分かれてきます。さらに範囲を大きくすると、ギャップの平均は全体として大きくなっていきます。それでも、ずっと小さいギャップが突然続いたり、急に大きな空白が出たりします。素数の間隔は気まぐれに見えるのに、全体ではちゃんと傾向があるのが面白いところです。
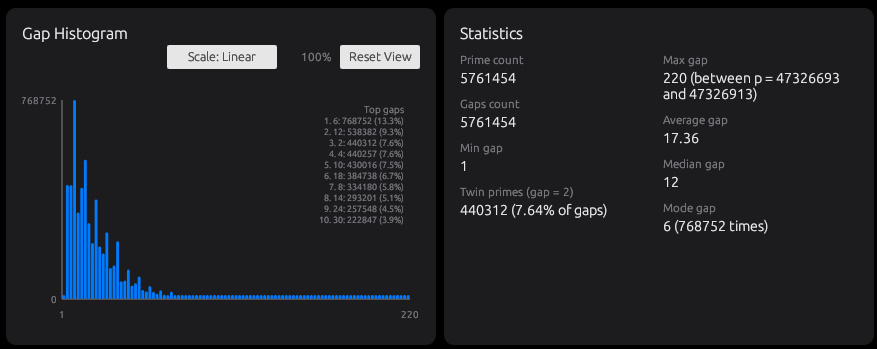
素数ギャップは、近くを見ると荒れているのに、別の角度で見ると形が整ってきます。そんな矛盾したような性格が、Gapタブで見えてきます。出やすいGapと出にくいGapがあって不思議ですね。
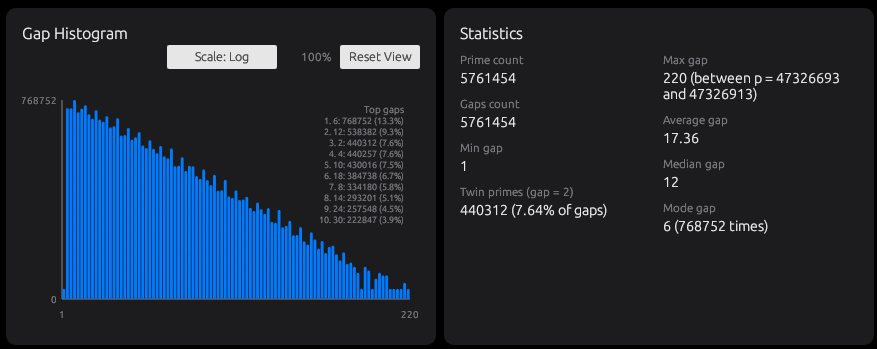
もしかしたら最大ギャップの大きな空白区間には何か秘密があるかもしれません。いちばん多いギャップ6の直後に出やすいギャップは何か、ギャップ6が連続する区間のあとに何か出現の癖があるかもしれません。
双子素数(ギャップ2)が多い区間と少ない区間があるなら、その偏りに未発見の癖が隠れているかもしれません。こうした小さな違和感を拾い集めていくと、何か新しい素数の振る舞いが見つかるかも。
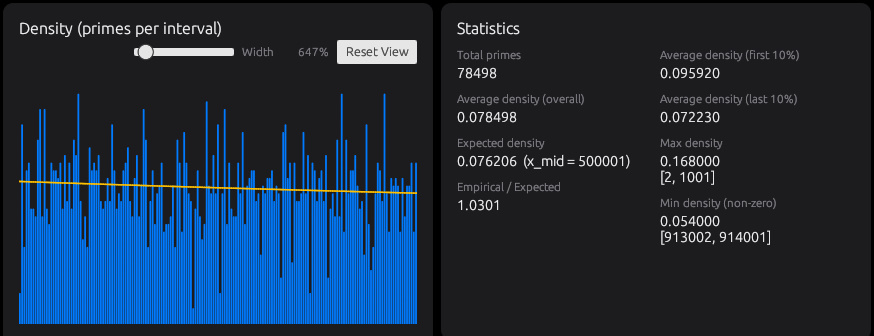
Densityタブで素数の出現ムラを体験
Densityタブでは、区間ごとに素数が何個出たかを数え、素数の密度をグラフにします。たとえば幅1000なら、1〜1000、1001〜2000のように区切って、それぞれの区間に素数が何個あるかを並べて見られます
素数は大きくなるほど出にくくなるので、密度は全体として下がっていきます。ところが、区間ごとに見ると、いつも同じように減っていくわけではなく、濃い区間と薄い区間が交互に出てきます。遠くから見ると減っていくのに、近くで見るとムラがある。素数は気まぐれに見えるのに、全体ではちゃんと傾向があるという不思議を、密度の波として体験できます。
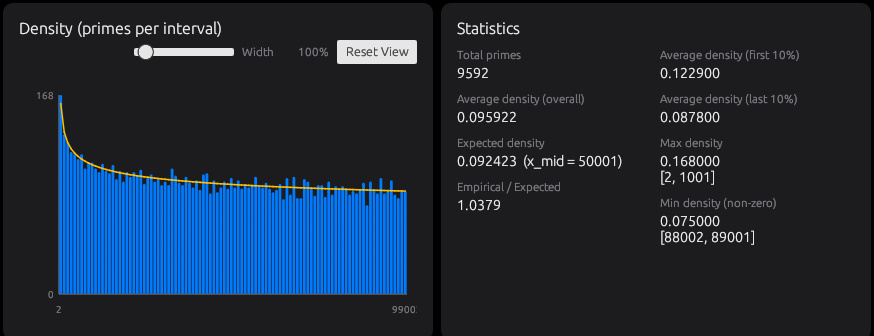
密度が急に低くなる谷はなぜ生まれるのか、密度が急に高くなる山は何が重なって起きているのか。密度の谷が続く区間では、Gapタブで大きなギャップが増えていないか、山が続く区間では双子素数が増えていないか、といった関係も見えてくるかもしれません。
区間幅を変えて同じ現象が残るかを確かめるのも面白く、こうした小さな違和感を拾い集めていくと、誰も発見していない法則が見つかるかもしれません。
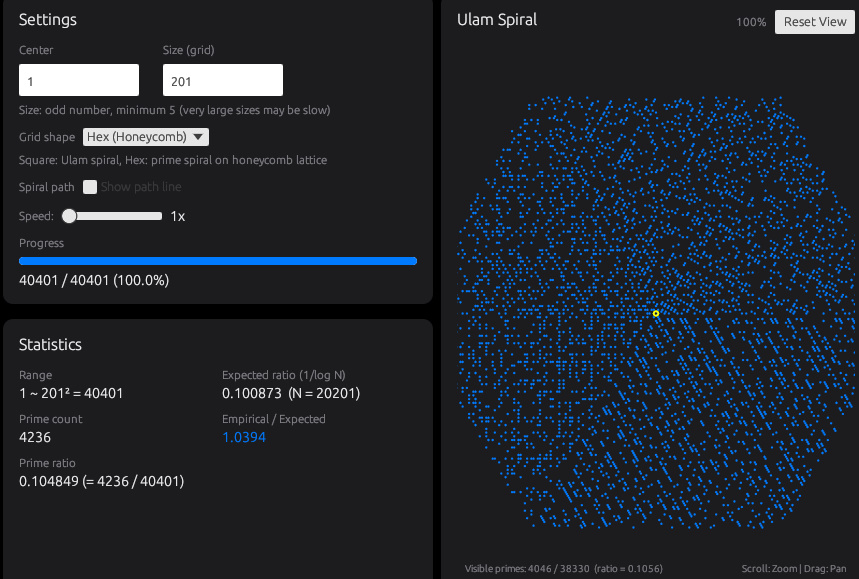
Spiralタブで素数の模様を体験
Spiralタブでは、数字をぐるぐる渦巻きの形に並べて、その中で素数だけを目印として表示します。数字を一直線に並べるのではなく、回転しながら外側へ広がる配置にすることで、素数がどこに集まりやすいのか、どこが空きやすいのかが模様として見えるようになります。
表示方法はSquare(Ulam)とHex(Honeycomb)を切り替えられ、同じ範囲でも格子の違いで模様の出方が変わるのも特徴です。必要に応じて渦巻きの経路線を重ねて表示し、数字がどの順番で配置されているかも確認できます。Ulamの渦はただ見ているだけでも楽しめます。
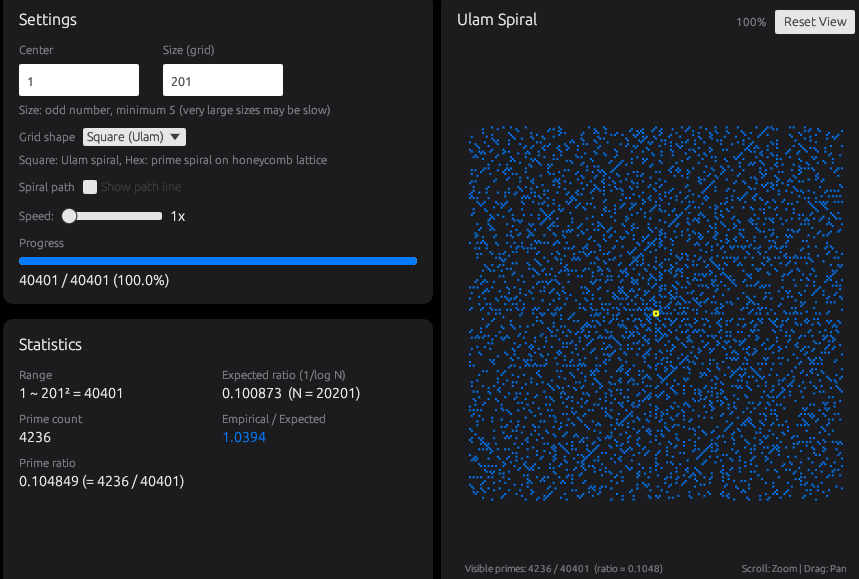
素数はランダム的なはずなのに、なぜか線や筋のように見えたり、逆にある方向だけ空いていたりします。この筋が見える理由は、そうなるのは明確な理由がありますが、どうしてそうなるのかを考えてみるのも面白いです。
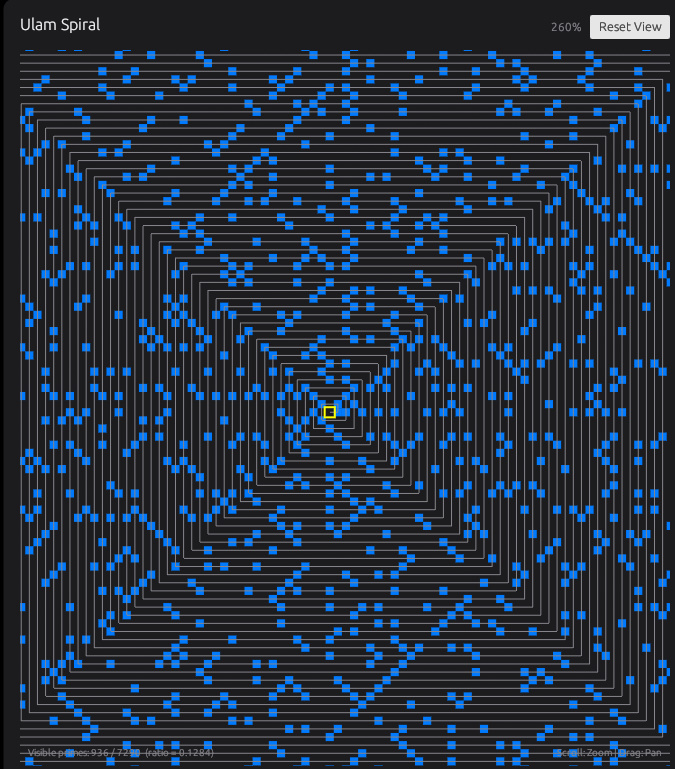
なぜ特定の方向には素数が少ないのか、筋が強く出る方向と弱い方向でどんな違いがあるのか。表示する範囲を広げたときに模様がどれくらい保たれるのか、SquareとHexで模様の出方はどう変わるのかといった観察もできます。いろいろ探してみると誰も発見していない法則を発見してしまうかもしれません。